AAAI2022に投稿した、“Fully Spiking Variational Autoencoder”についての公式の解説記事です。

Abstract

• Spiking Neural Network (SNN)を用いてVAEを構築
• 通常のANNと同等かそれ以上の精度で画像生成ができることを確認した

• Arxiv
• Github

---

はじめに

Spiking Neural Network (SNN) は人間の脳をより正確に模倣したニューラルネットワークです。 その特徴としては、

• 生体脳のニューロンモデルを使用している
• 全ての特徴量はスパイク列と呼ばれる0,1の時系列データで表現される
• Neuromorphic deviceという専用のデバイス上では超高速かつ超低消費電力で動作する

という点が挙げられます。詳しくはSpiking Neural Network解説を参照してください。

以上の特性から、SNNは多くの実応用が期待されていますが、発展途上の分野ということもあり、SNNによる生成モデルの研究はほぼ存在しません(一応、Spiking-GANという論文が存在しますが、現実的なレベルで画像生成ができているとは言えません)

しかし、将来的にSNNがエッジデバイスや自動運転など、さまざまな場面で活用されることを考えると、SNNによる生成モデルを構築することは非常に重要です。SNNの高速かつ低消費電力の特性から、あらゆるウェアラブルデバイスで高精度のAIの利用が可能になったり、SNNを組み込んだロボットが自立的に街中で活躍する未来につながるかもしれません。

そこで今回我々は、SNNを用いて生成モデルの一つであるVAE(Variational Autoencoder)を構築することを目指します

Spiking Neural Networkについて

SNNではLeaky-Integrate-and-Fire (LIF) neuronというニューロンモデルを使うことが一般的です。LIF neuronに入力スパイク列が入力されると、それに対してシナプスの結合重み$w$が掛け合わされて電流となり、LIF neuronの膜電位 (membrane potential)が時間的に変化します。

膜電位がある閾値$V_{th}$を超えると、その時刻でスパイクを発火し、膜電位はゼロにリセットされます。このようにして、LIF neuronはスパイク列を受け取りスパイク列を出力しています。

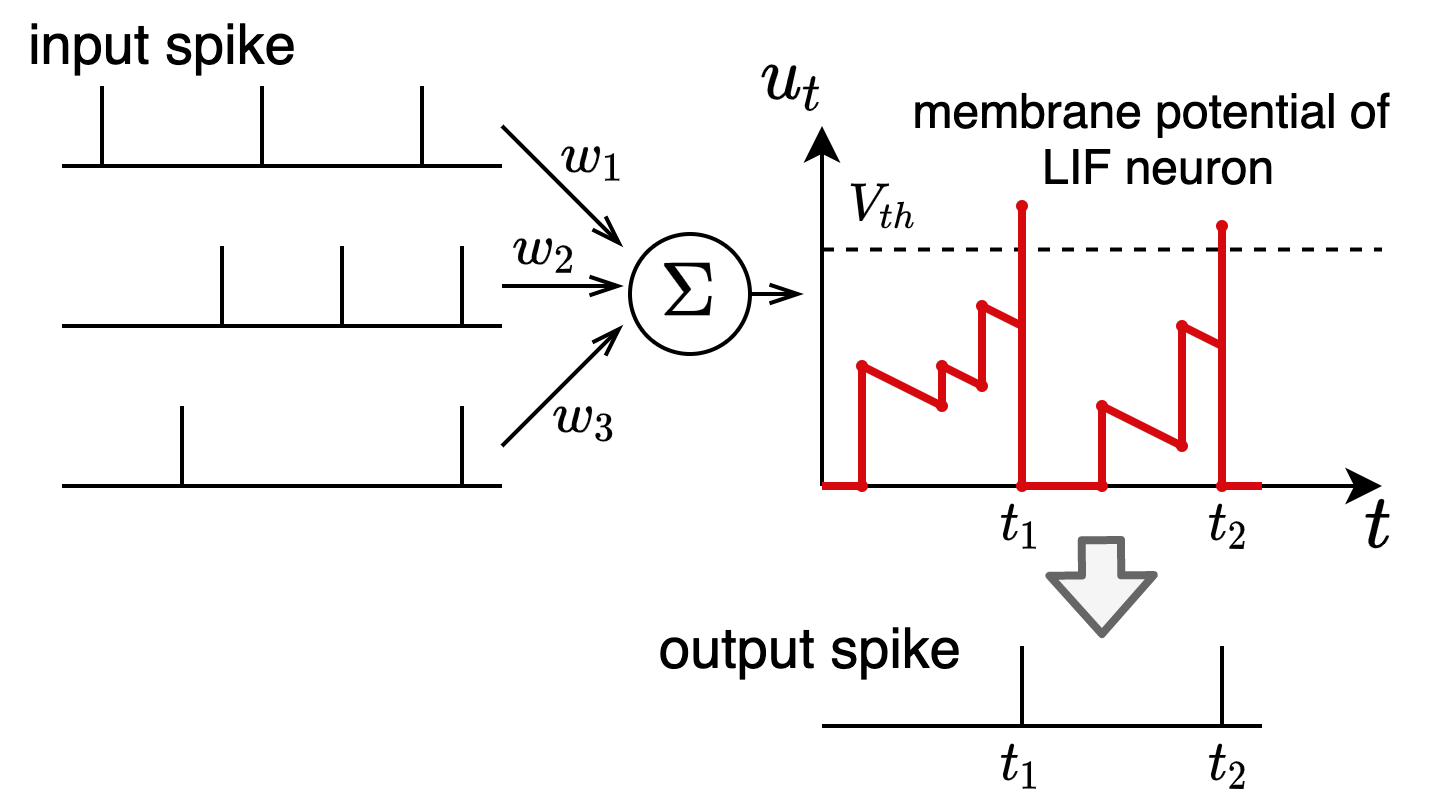
LIF neuronの様子を定式化すると以下のようになります。

\[\begin{align*} u_{t,n} &= \tau_{\mathrm{decay}} u_{t-1,n}(1-o_{t-1,n}) + \sum_j w^j o_{t,n-1}^j \label{eq:mem}\\ o_{t,n} &= H(u_{t,n}-V_{\mathrm{th}}) \label{eq:heaviside} \end{align*}\]

$u_{t,n}$は第$n$層で時刻$t$の時の膜電位、$o_{t,n}$は対応する出力スパイクです。$H$はヘヴィサイドのステップ関数であり、$u_{t,n}$が$V_{\mathrm{th}}$を超えたときに発火し、$1$を出力するようになっています。

$w^j$は前のニューロンとのシナプス結合重みであり、この繋ぎ方を変更することで、通常のニューラルネットワークと同様に、全結合層や畳み込み層を実現することが可能です。

この$w^j$を誤差逆伝播法で学習することを考えます。その際、ヘヴィサイドのステップ関数が微分不可能であることが問題となりますが、現在最も良い認識精度を達成している[Zheng+, AAAI2021]では、これの微分を以下のように近似しています。

\[\begin{align*} \frac{\partial o_{t,n}}{\partial u_{t,n}} = \frac{1}{a} \mathrm{sign}\left(|u_{t,n} - V_{\mathrm{th}}|< \frac{a}{2}\right) \end{align*}\]

$a$は近似関数形を決定するパラメータで、今回は$0.2$に設定しています。これにより、誤差逆伝播法の近似を用いてSNNを学習することが可能になります。

Variational Autoencoderについて

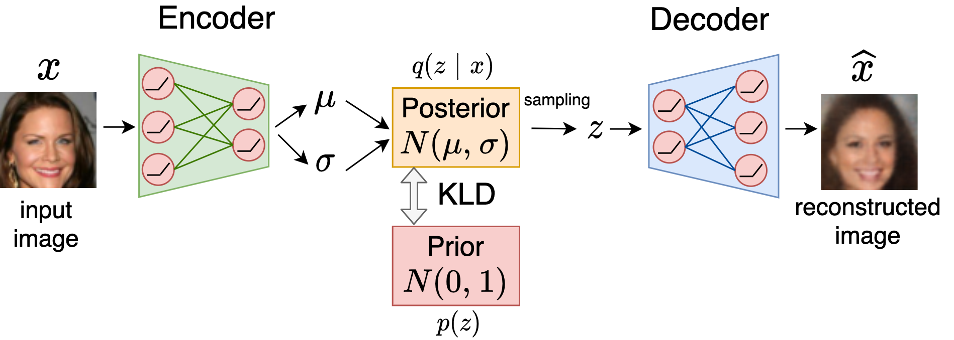
Variational Autoencoder (VAE) は潜在空間の分布を明示的に仮定した生成モデルです。入力画像$x$からEncoderは正規分布のパラメータ$\mu, \sigma$を生成し、$\mathcal{N}(\mu, \mathrm{diag(\sigma)})$を事後分布$q(z|x)$とします。そこからの潜在変数$z$のサンプリングは, reparameterization trickを用いて以下のように行います。

\[\begin{align} z = \mu + \sigma \odot \epsilon ~~\mathrm{s.t.} ~~ \epsilon \sim \mathcal{N}(0,1) \end{align}\]

潜在変数$z$はDecoderに入力され、再構成画像$\hat{x}$を得ます。 学習は、対数尤度の下限である以下のELBOを最大化して行います。

\[\begin{align} \mathrm{ELBO} = \mathbb{E}_{q(z|x)}[\log p(x|z)] - \mathrm{KL}[q(z|x)||p(z)] \end{align}\]

$p(z)$は潜在変数の事前分布であり、通常は$\mathcal{N}(0,1)$に設定します。

VAEは生成モデルの中でも学習が安定しており、最近では非常に高精細な画像生成も可能になっています。また、VAE は生体脳の学習則にも深く結びついていることが知られているため、今回は、SNNでVAEを構築することを目指します

提案手法: Fully Spiking Variational Autoencoder

今回の壱万の問題点は、上記のreparameterization trickを用いた実数値の潜在変数のサンプリングは、スパイク列のみを扱うSNNでは実行できないことです。

そこで今回、SNNの出力からランダムに選択することで、潜在スパイク列を逐次的にサンプリングする手法、Autoregressive Bernoulli spike samplingを提案します。

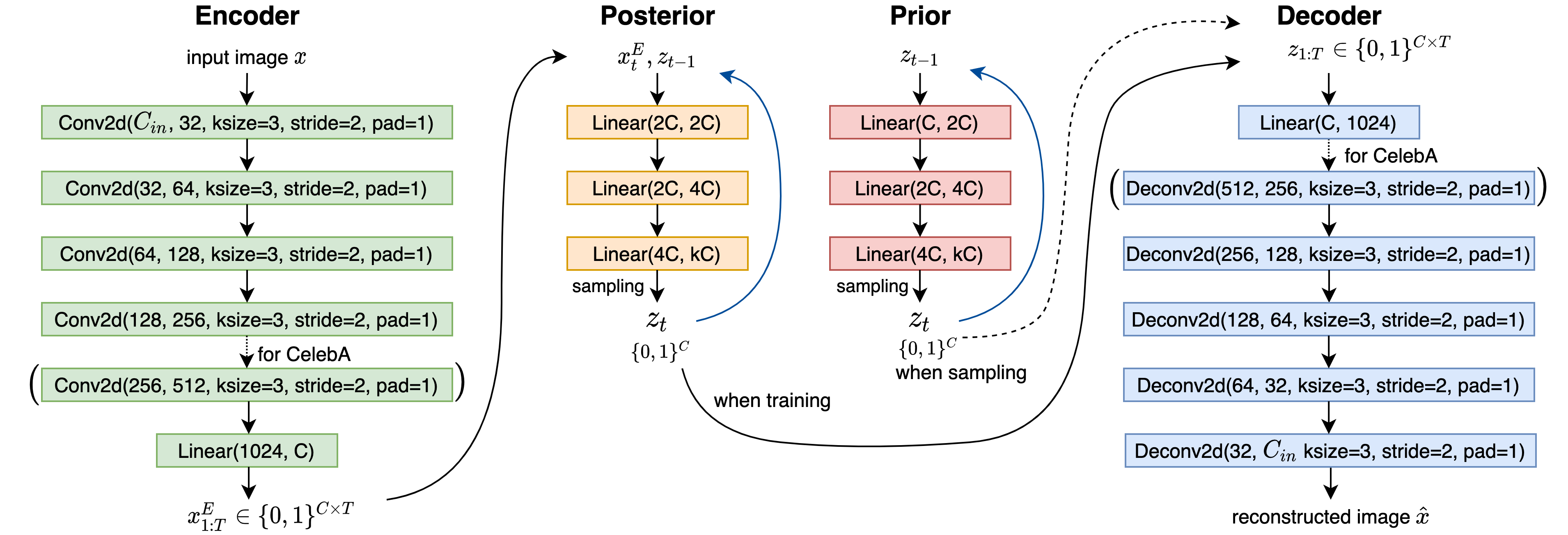
まず提案するFully Spiking Variational Autoencoder (FSVAE)の全体図は以下になります。

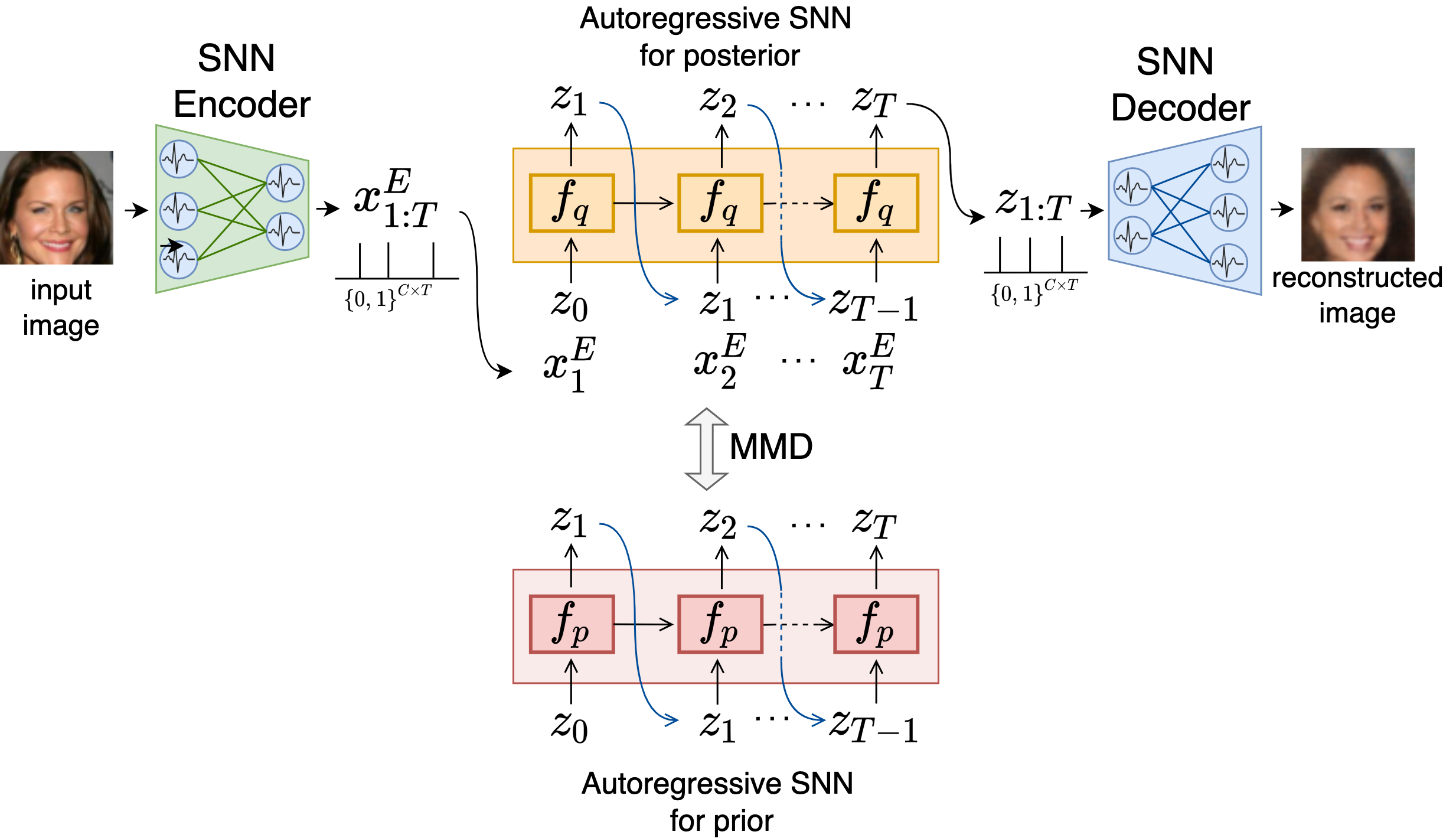
入力画像$x$はSNN Encoderに入力され、スパイク列の特徴量$\boldsymbol{x}^E_{1:T}$を得ます。

posteriorでは、$\boldsymbol{x}^E_t$と前の時刻の潜在スパイク$\boldsymbol{z}_{t-1}$を用いて、Autoregressive SNN $f_q$から逐次的に$\boldsymbol{z}_t$をサンプリングします。このサンプリング方法を、Autoregressive Bernoulli spike samplingと名付け、下で説明します。

一方priorでは、$\boldsymbol{x}^E_t$は使用せずにサンプリングを行います。

サンプリングされた$\boldsymbol{z}_{1:T}$はSNN Decoderに入力され、再構成画像$\hat{x}$を得ます。

Autoregressive Bernoulli spike sampling

潜在スパイク列 $\boldsymbol{z}_{1:T}$のサンプリング方法を説明します。

まず入力は、posteriorの場合は $x^E_t$と $z_{1:T}$、priorの場合は$z_{t-1}$のみになります。それをあるSNNに入力し、出力次元を$k$倍に拡大します。よって、このSNNの出力は$kC$個の$0,1$のデータになりますが、ここから図のように$k$個ごとに一つランダムに選択して、それを$\boldsymbol{z}_t$とします。

これによって、単にランダムに選択しているだけですが、対応するBernoulli分布と同等のサンプリングを行うことができます。実際下図では、\(Ber([\frac{2}{3}, 1, \frac{1}{3}])\)からのサンプリングに等しいです。

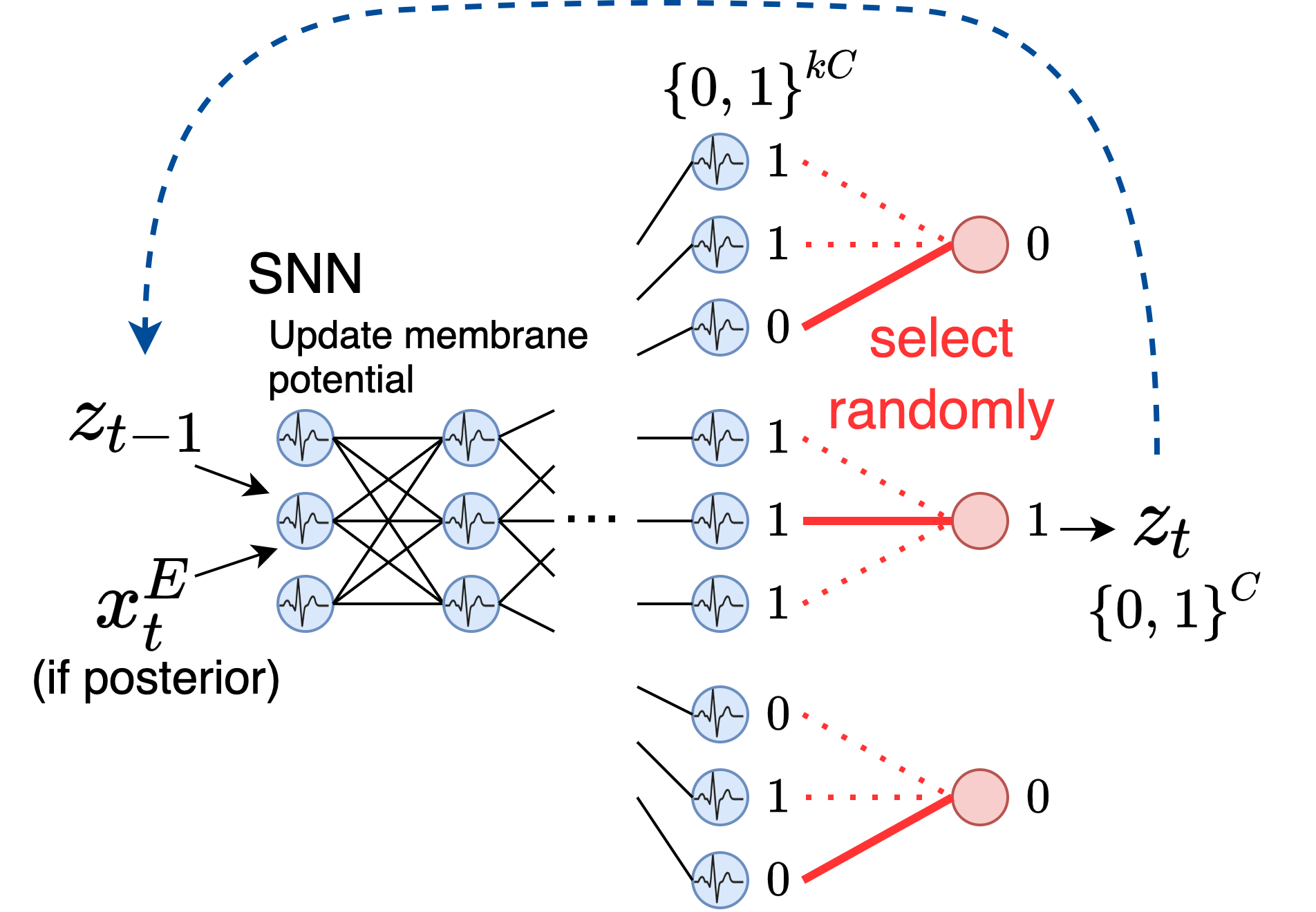
Autoregressive Bernoulli spike samplingによって、潜在分布は(非定常)ベルヌーイ過程になります。 事後分布$q$と事前分布$p$は以下のように書けます。

\[\begin{align} q(\boldsymbol{z}_{1:T} | \boldsymbol{x}_{1:T}) &= \prod_{t=1}^T q(\boldsymbol{z}_t | \boldsymbol{x}_{\leq t}, \boldsymbol{z}_{<t}) = \prod_{t=1}^T Ber(\boldsymbol{\pi}_{q,t}) \\ p(\boldsymbol{z}_{1:T}) &= \prod_{t=1}^T p(\boldsymbol{z}_t | \boldsymbol{z}_{<t}) = \prod_{t=1}^T Ber(\boldsymbol{\pi}_{p,t}) \end{align}\]

Loss function

ELBOは通常のVAEと同様に計算できます。

\[\begin{align} ELBO =& \mathbb{E}_{q(\boldsymbol{z}_{1:T}|\boldsymbol{x}_{1:T})}[\log p(\boldsymbol{x}_{1:T}|\boldsymbol{z}_{1:T})] - \mathrm{KL}[q(\boldsymbol{z}_{1:T}|\boldsymbol{x}_{1:T})||p(\boldsymbol{z}_{1:T})] \label{ELBO} \end{align}\]

この第一項は通常のVAEと等しくMSE(平均二乗和誤差)として書けます。今回は、第二項のKL divergenceの代わりにMMD (Maximum-mean-discrepancy)を使用します。その理由には以下があります。

• KL divergenceは発散しやすく学習が難しいこと
• 先行研究のMMD-GLM [Arribas, Zhao,and Park, NeurIPS2020]で、MMDの方がKLDよりもスパイク列の分布間距離として良いことが知られていること

MMDはカーネル関数$k$を用いて以下のように書けます。

\[\begin{align} \mathrm{MMD}^2[q(\boldsymbol{z}_{1:T}|\boldsymbol{x}_{1:T}),p(\boldsymbol{z}_{1:T})] =\underset{\boldsymbol{z},\boldsymbol{z}'\sim q}{\mathbb{E}}[k(\boldsymbol{z}_{1:T},\boldsymbol{z}'_{1:T})] +\underset{\boldsymbol{z},\boldsymbol{z}'\sim p}{\mathbb{E}}[k(\boldsymbol{z}_{1:T},\boldsymbol{z}'_{1:T})] -2\underset{\boldsymbol{z}\sim q,\boldsymbol{z}'\sim p}{\mathbb{E}}[k(\boldsymbol{z}_{1:T},\boldsymbol{z}'_{1:T})] \label{eq:mmd} \end{align}\]

今回$k$は、MMD-GLMのmodel based kernelを踏襲して、\(k(\boldsymbol{z}_{1:T},\boldsymbol{z}'_{1:T})=\sum_t \mathrm{PSP}(\boldsymbol{z}_{\leq t})\mathrm{PSP}(\boldsymbol{z}'_{\leq t})\) のように設定します。

ここで$\mathrm{PSP}$は、シナプス後ポテンシャル関数(postsynaptic potential funciton)であり、スパイク列の時系列性を考慮することができます。今回は$\mathrm{PSP}$として、[Zhang+, NeurIPS2020]で使用されている first-order synaptic modelを使用し、以下の更新式で$\mathrm{PSP}(\boldsymbol{z}_{\leq t})$を計算します。

\[\begin{align} \mathrm{PSP}(\boldsymbol{z}_{\leq t}) = \left( 1-\frac{1}{\tau_{\mathrm{syn}}}\right) \mathrm{PSP}(\boldsymbol{z}_{\leq t-1}) + \frac{1}{\tau_{\mathrm{syn}}}\boldsymbol{z}_t \label{eq:psp} \end{align}\]

$\tau_{\mathrm{syn}}$はシナプス時定数であり、$\mathrm{PSP}(\boldsymbol{z}_{\leq 0})=0$とします。

これによって、MMDは以下のように計算できます。

\[\begin{align} &\mathrm{MMD}^2[q(\boldsymbol{z}_{1:T}|\boldsymbol{x}_{1:T}),p(\boldsymbol{z}_{1:T})]\nonumber\\ =& \sum_{t=1}^T \| \mathrm{PSP}(\underset{\boldsymbol{z}\sim q}{\mathbb{E}}[\boldsymbol{z}_{\leq t}]) - \mathrm{PSP}(\underset{\boldsymbol{z}\sim p}{\mathbb{E}}[\boldsymbol{z}_{\leq t}]) \|^2 \\ =& \sum_{t=1}^T \| \mathrm{PSP}(\boldsymbol{\pi}_{q,\leq t}) - \mathrm{PSP}(\boldsymbol{\pi}_{p,\leq t})\|^2 \end{align}\]

以上により、全体の損失関数は次のようになります。

\[\begin{align} \mathcal{L} = \mathrm{MSE}(x,\hat{x}) + \sum_{t=1}^T \| \mathrm{PSP}(\boldsymbol{\pi}_{q,\leq t}) - \mathrm{PSP}(\boldsymbol{\pi}_{p,\leq t})\|^2 \label{eq:lossmmd} \end{align}\]

実験

データセット

MNIST, FashionMNIST, CIFAR10, CelebAを使用しています。

アーキテクチャー

EncoderとDecoderは5層か6層のSpiking CNNを使用し、priorとposteriorは3層のSNNを用いています。

比較手法

比較手法として、同じ構造のEncoderとDecoderを持つ通常のVAEを用いました。これを全く同じ実験設定で学習して評価しました。

定性評価

生成画像は以下のようになります。どのデータセットでも、提案手法が同等以上のクオリティで生成できていることがわかります。

定量評価

定量評価を行っても、提案手法の方が通常のVAEを上回っていることがわかります。 評価指標は、

• 再構成誤差
• Inception score
• FID
• 各データセットで事前学習されたAutoencoderの潜在変数のFrechet distance

の4つです。

再構成誤差とInception scoreに関しては、全てのデータセットで提案手法の方が上回っており、またFIDはMNIST, FashionMNIST, CIFAR10で上回り、AutoencoderのFrechet distanceはFashionMNIST, CIFAR10, CelebAで上回っています。

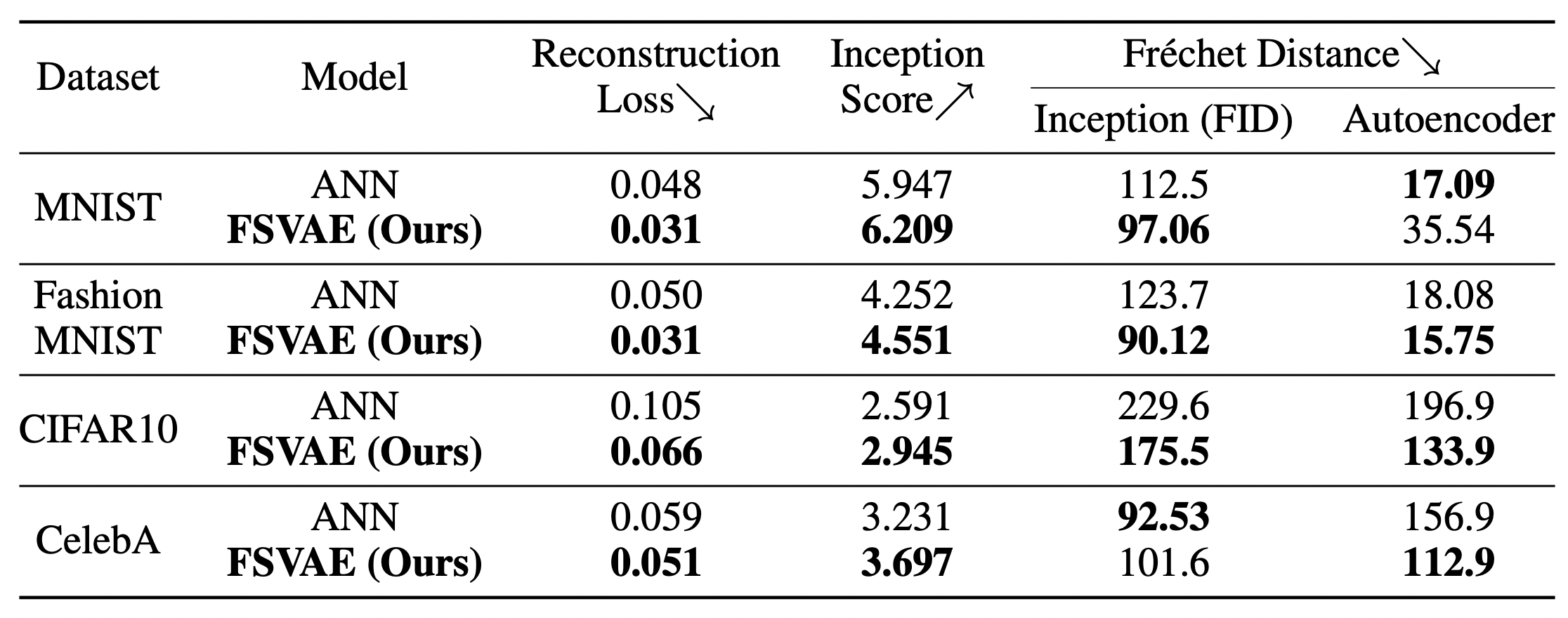
計算コストの比較

MNISTの画像一枚の処理にかかる計算コストも比較しました。浮動小数点の足し算は提案手法の方が6.8倍ほど多いですが、掛け算の回数は1/13になっています。一般に掛け算の方が計算コストが大きいため、計算コストの点からも提案手法の方が良いと言えます。

また、将来的に提案手法はNeuromorphic deviceに組み込むことが可能のため、大幅な計算コストの改善も期待できます。

まとめ

この論文では、モデル全体をSNNで構築した、Fully Spiking Variational Autoencoderを提案し、通常のVAEと同等かそれ以上の画像生成を可能にしました。今回は5,6層の浅いモデルを用いましたが、今後の最近の高解像度のVAE手法を応用することで、さらなる改善が期待できます。